- 声学楼论坛 (http://874085.11480.vipsjym.com.my3w.com/bbs/index.asp)
-- 基础理论室 (http://874085.11480.vipsjym.com.my3w.com/bbs/list.asp?boardid=17)
---- [原创]关于传声器与扬声器的思考 (http://874085.11480.vipsjym.com.my3w.com/bbs/dispbbs.asp?boardid=17&id=17308)
-- 发布时间:2009-10-25 20:22:25
-- [原创]关于传声器与扬声器的思考
本人是一个业余音响爱好者,有些疑问一直困扰着我百思不得其解,恳请声学楼的老师指导一下。
1、录音环节。电信号的瞬时值记录的是声波信号的质点瞬时振动速度?还是瞬时振幅?还是瞬时声压?
传声器按工作原理的不同分为动圈式传声器、电容传声器、压电陶瓷传声器。对于动圈式传声器和电容传声器结构上都有一个能随空气振动的振膜,理想的振膜质量应该轻到可忽略不计,可以视为空气分子,振膜置于声场中做受迫振动的运动状态与空气质点的振动完全一致。但动圈式传声器和电容传声器声电转换原理不同。对电容传声器输出电压正比于电容变化量,而电容变化量的又正比于振膜的位移,因此电容传声器输出电压信号记录的是振膜的瞬时振幅,也就是空气分子的瞬时振幅;而动圈式传声器输出电压信号正比于线圈切割磁场的速度(U=BLV),因此动圈式传声器输出电压信号记录的是振膜的瞬时振动速度,即空气质点的瞬时振动速度。而压电陶瓷传声器输出电压信号则正比于施加于传感器上的压力,因此记录的是瞬时声压。
不同的传声器因为其性能的不同而用在不同的场合,对于一首歌的录制,鼓声也许是用动圈式传声器录制的,人声也许是电容传声器录制的。问题来了,动圈式传声器输出信号记录的是声波质点的瞬时振动速度,而电容传声器输出信记录的是声波质点的瞬时振幅。这两种记录不同信息的信号在音乐的制作中如何混在一起?他们之间是否要需要转换为同一形式然后再叠加?如果需要的话,最终转化为振动速度?瞬时振幅?还是瞬时声压?还是其他信号,有规定吗?还是声波信号不关心这个问题而直接叠加?
2、放声环节。对于动圈式扬声器,电声转换原理是U=BLV,对于理想的动圈式扬声器,输入一定的电压,平衡状态它输出的是振膜的运动速度。但实际的扬声器振动质量都很大,很难做到理想,对扬声器输入一定的电压,它只能输出振膜的加速度。
要高保真的回放音乐我们是不是要把录音与放音器材来统一考虑呢?我觉得如果能够把传声器振膜的振动拷贝到扬声器鼓纸上来就能实现高保真回放。既然扬声振膜是电压到振动加速度的转换,那么传声器信号是不是应该转换为瞬时加速度呢?对动圈式信号是速度要进行一次微分,而电容信号是位移信号要进行二次微分。实际录音是不是进行这些处理呢?
这是我的一些疑问,希望各位老师能指点指点,也希望能给大家一个启发。

-- 发布时间:2009-10-26 9:27:36
--
把录音与放音器材来统一考虑是正确的,同时还要考虑录放声的环境.
这些(电声)器件,只是完成了能量的转换,所以统称换能器,如声能(主要是声压)转换成机械能,再转换成电(磁)能.这个过程是可逆的.
至于换能原理,其实有多种.如传声器也有动圈式的,扬声器也有静电式的.不能说哪种方式更保真或更优越.
-- 发布时间:2009-10-26 12:49:45
--
这个关于扬声器和传声器物理原理的问题很好,涉及到两者的详细物理背景
即使是熟悉物理知识的网友也可能一时反应不过来,“基础理论室”最需要的就是这样的帖子
在原帖里,作者提到电声和声电转换中涉及的声物理量问题;我理解这个问题
的确,从换能原理的公式出发,如电容式的位移转换为电压,一定是没错的
问题在哪?在于换能方式不是“声电”而是“声——力——电”
力学系统被原作者忽略掉了;而它自身是有个力阻抗的,跟电路里的电容、电感一样,有积分或微分的效果
实际上使用的多数声传感器捕捉的都是声压信号,路端电压的波形对应于声波波形;灵敏度说的都是dB/V
所以不存在所谓的“不同原理的传声器信号不好叠加”的问题
你理解的那个“积分”或“微分”的转换是通过力学部分的设计,通过控制质量、弹性和阻尼元件的相对关系来实现的
具体可参看《声学基础》1.5,或管老师的《电声技术基础》
换句话说,你的下面两个假设是不成立的:
“振膜置于声场中做受迫振动的运动状态与空气质点的振动完全一致”
“振膜的瞬时振幅,也就是空气分子的瞬时振幅”
这个成立的前提是系统没有弹性,质量为0,刚性无限大
紧贴振膜表面的那一层气体微元的运动状态倒的确是和振膜一致的
但是,这个运动状态受到了振膜本身的调制,并不是待测状态本身
空气微元的运动状态传递到振膜的运动状态,不是无条件的
具体发生什么变化,还取决于振膜的力阻抗
一个小错误是,扬声器所依据的基本换能原理是F=Bli
B——磁感应强度
l——音圈导线总长度
i——电流
U=BLV在这里仍然其作用,不过得到的是感生电动势
另一个小错误,扬声器振膜的质量相对较大,这个不是技术手段做不到更低
扬声器工作在所谓“质量控制区”,质量不能太低的
另外,回楼下的,俺怀疑你是否真把这个“走路问题”弄明白了,你至少没讲明白吧
[此贴子已经被作者于2010-04-02 10:20:32编辑过]
-- 发布时间:2009-10-27 13:11:02
--
由于中文的暧昧,使得我们理解很吃力,你问的这些问题都是很简单的入门,如同小孩学走路,每样东西都要理解透彻。
首先要记录一个声音,就要能采集到该声音的频率和声压。
假如采集的声音是100HZ的频率,不管是那种话筒它的振膜震动频率也会是100HZ,这点我相信你不会有疑问。
而采集声音的声压就有几种方式,不管是用什么方式(动圈,电容,压电)最终的结果就是要得到声压的大小。
而你之所以迷惑的地方在于声压,压力,运动速度,振幅,等这些参数的模糊-----声压正比运动速度正比振幅正比压力所以这几个只要记录其中一个就能得到声压,由此可知这些都可以看成是同一东西,而你却偏要以为是不同的东西,而频率和这些参数无关,你却以为这些和频率有关。
-- 发布时间:2009-10-27 17:40:53
--
这里,赞同楼上的观点.
-- 发布时间:2009-10-30 23:18:24
--
以下是引用老兔子在2009-10-27 13:11:02的发言:
由于中文的暧昧,使得我们理解很吃力,你问的这些问题都是很简单的入门,如同小孩学走路,每样东西都要理解透彻。
首先要记录一个声音,就要能采集到该声音的频率和声压。
假如采集的声音是100HZ的频率,不管是那种话筒它的振膜震动频率也会是100HZ,这点我相信你不会有疑问。
而采集声音的声压就有几种方式,不管是用什么方式(动圈,电容,压电)最终的结果就是要得到声压的大小。
而你之所以迷惑的地方在于声压,压力,运动速度,振幅,等这些参数的模糊-----声压正比运动速度正比振幅正比压力所以这几个只要记录其中一个就能得到声压,由此可知这些都可以看成是同一东西,而你却偏要以为是不同的东西,而频率和这些参数无关,你却以为这些和频率有关。
谢谢老兔子的关注,“声压正比运动速度正比振幅正比压力所以这几个只要记录其中一个就能得到声压”这我是同意的。的确,无论对那个量进行测量我们都能完整的记录声波信息;但是问题是他们记录的方式不同,而我们的放声系统就一种,无法适应这多变的信号。附件上的图片很好的说明了问题的存在。对于一个做正弦振动的音源,无论是使用动圈式传声器还是电容传声器对声音进行录音,我们都能得到相同的回放声音。但是对于一个做矩形波振动的音源,两种传声器的录音就会产生差别。
由于中文的暧昧,使得我们理解很吃力,你问的这些问题都是很简单的入门,如同小孩学走路,每样东西都要理解透彻。
首先要记录一个声音,就要能采集到该声音的频率和声压。
假如采集的声音是100HZ的频率,不管是那种话筒它的振膜震动频率也会是100HZ,这点我相信你不会有疑问。
而采集声音的声压就有几种方式,不管是用什么方式(动圈,电容,压电)最终的结果就是要得到声压的大小。
而你之所以迷惑的地方在于声压,压力,运动速度,振幅,等这些参数的模糊-----声压正比运动速度正比振幅正比压力所以这几个只要记录其中一个就能得到声压,由此可知这些都可以看成是同一东西,而你却偏要以为是不同的东西,而频率和这些参数无关,你却以为这些和频率有关。
谢谢老兔子的关注,“声压正比运动速度正比振幅正比压力所以这几个只要记录其中一个就能得到声压”这我是同意的。的确,无论对那个量进行测量我们都能完整的记录声波信息;但是问题是他们记录的方式不同,而我们的放声系统就一种,无法适应这多变的信号。附件上的图片很好的说明了问题的存在。对于一个做正弦振动的音源,无论是使用动圈式传声器还是电容传声器对声音进行录音,我们都能得到相同的回放声音。但是对于一个做矩形波振动的音源,两种传声器的录音就会产生差别。
 此主题相关图片如下:纯音.jpg
此主题相关图片如下:纯音.jpg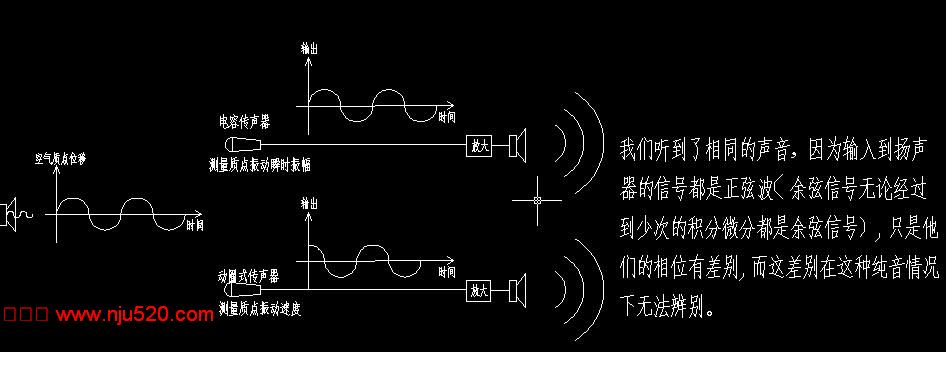
 此主题相关图片如下:矩形波.jpg
此主题相关图片如下:矩形波.jpg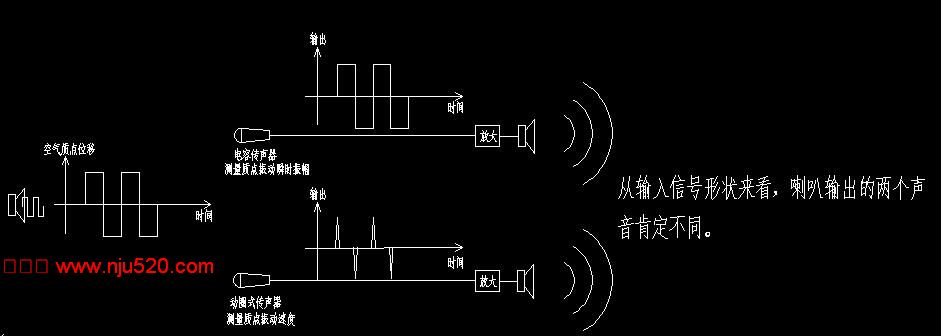
-- 发布时间:2009-11-1 14:45:42
--
谢谢arch的指点,请问,对于扬声器振膜表面声压与振膜振动速度是同相的吗?还是与振膜加速度同相?
-- 发布时间:2009-11-8 15:05:31
--
我没做过试验,但我以为动圈话筒不会出现你所讲的现象,举例分析:
假如我们给扬声器加上1V的电压1秒钟,假设扬声器纸盆向外运动,扬声器纸盆运动速度是1米每秒,那么扬声器纸盆会向外运动持续一秒钟到1米处停止,扬声器纸盆的对面有个动圈话筒,那么该动圈话筒振膜会被扬声器持续向内推动到1米距离,振膜运动速度是1米每秒,持续输出1秒钟的电压1V------准确的记录了1V1秒的信号。
假如我们给扬声器加上2V的电压1秒钟,假设扬声器纸盆向外运动,扬声器纸盆运动速度变成2米每秒,那么扬声器纸盆会向外持续运动到2米处停止,扬声器纸盆对面有个动圈话筒,那么该动圈话筒振膜会持续向内运动2米,速度是2米每秒,输出电压2V-----同样会准确的记录2V1秒的信号。
条件同上,假设扬声器对面放的是电容话筒,1V 1秒的情况下扬声器持续向外运动1秒钟,给电容话筒持续施加1压力1秒,2V1秒的情况下扬声器持续向外运动1秒,给电容话筒持续施加2压力1秒,电容话筒同样会准确的记录。
所以你以为动圈话筒不能记录脉冲是不正确的,可能源于你想象中的动圈话筒是有“冲程"限制,假如你把动圈话筒想象成无限“冲程”的,就可以理解动圈话筒也能记录脉冲。
-- 发布时间:2009-11-9 14:58:30
--
以下是引用老兔子在2009-11-08 15:05:31的发言:
我没做过试验,但我以为动圈话筒不会出现你所讲的现象,举例分析:
假如我们给扬声器加上1V的电压1秒钟,假设扬声器纸盆向外运动,扬声器纸盆运动速度是1米每秒,那么扬声器纸盆会向外运动持续一秒钟到1米处停止,扬声器纸盆的对面有个动圈话筒,那么该动圈话筒振膜会被扬声器持续向内推动到1米距离,振膜运动速度是1米每秒,持续输出1秒钟的电压1V------准确的记录了1V1秒的信号。
这段话里面,对的成分很少啊
头次听说扬声器和传声器是“你拍一,我拍一”的关系呢
没有电力声转换的基本概念
没有力学响应的基本概念
没有声辐射的基本概念
没有声接收的基本概念
......
-- 发布时间:2009-11-9 16:08:33
--
以下是引用binbin在2009-11-01 14:45:42的发言:
谢谢arch的指点,请问,对于扬声器振膜表面声压与振膜振动速度是同相的吗?还是与振膜加速度同相?
谢谢arch的指点,请问,对于扬声器振膜表面声压与振膜振动速度是同相的吗?还是与振膜加速度同相?
这个问题虽然很简单,但也是一个非常好的问题
概括一下,你说的其实是:“当扬声器振膜表面的振速和相位已知,场点上的相位为何”
回答是:扬声器振膜表面声压与振膜振动速度一般是不同相位的,具体的情况取决于频率
电声学里有个辐射阻抗的概念,这个阻抗可以分离出“幅值”和“相位”的
其中的“相位”代表的,就是振膜表面声压与振膜振动速度随着频率的变化趋势
我给你个好东西,你看看192电子页的《声辐射》和图3-22
http://222.200.98.136/data/017/015/00539968/otiff/otiff.djvu
只谈论现象的话,首先要明白同一时刻,声场里各个场点上的声压相位并不一致,讨论确定场点的相位才有意义
点确定了以后,可以说:由于空气有粘滞力,刚好紧贴着振膜的那层空气分子总是与振膜是一个运动状态
不过往外一点点,由于空气具有弹性和质量,两者的相位就不同了
场点上的声压是来自振膜各点的同向辐射相互叠加的结果
但是振膜各点到场点的距离不一致
因而计算近距离,或曰近场相位的时候,还要考虑这个叠加问题
...绕过了贝赛尔函数,不过按照我的普及能力,似乎绕不过多元微积分了
-- 发布时间:2009-11-9 16:28:27
--
以下是引用arch在2009-11-09 14:58:30的发言:
这段话里面,对的成分很少啊
头次听说扬声器和传声器是“你拍一,我拍一”的关系呢
没有电力声转换的基本概念
没有力学响应的基本概念
没有声辐射的基本概念
没有声接收的基本概念
......
 我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。
我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。
而我提出的理论重点是“动圈话筒振膜冲程想象成无限”“电容话筒振膜想象成无冲程”这样就能理解动圈话筒通过记录音圈移动速度同样是可以记录脉冲。
而你提出的什么声学的基本概念和我要论述的道理有关系吗?真的有关系吗?是不是真的有关系了?
这段话里面,对的成分很少啊
头次听说扬声器和传声器是“你拍一,我拍一”的关系呢
没有电力声转换的基本概念
没有力学响应的基本概念
没有声辐射的基本概念
没有声接收的基本概念
......
 我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。
我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。而我提出的理论重点是“动圈话筒振膜冲程想象成无限”“电容话筒振膜想象成无冲程”这样就能理解动圈话筒通过记录音圈移动速度同样是可以记录脉冲。
而你提出的什么声学的基本概念和我要论述的道理有关系吗?真的有关系吗?是不是真的有关系了?
-- 发布时间:2009-11-16 2:11:00
--
以下是引用arch在2009-11-09 16:08:33的发言:
这个问题虽然很简单,但也是一个非常好的问题
概括一下,你说的其实是:“当扬声器振膜表面的振速和相位已知,场点上的相位为何”
回答是:扬声器振膜表面声压与振膜振动速度一般是不同相位的,具体的情况取决于频率
电声学里有个辐射阻抗的概念,这个阻抗可以分离出“幅值”和“相位”的
其中的“相位”代表的,就是振膜表面声压与振膜振动速度随着频率的变化趋势
只谈论现象的话,首先要明白同一时刻,声场里各个场点上的声压相位并不一致,讨论确定场点的相位才有意义
点确定了以后,可以说:由于空气有粘滞力,刚好紧贴着振膜的那层空气分子总是与振膜是一个运动状态
不过往外一点点,由于空气具有弹性和质量,两者的相位就不同了
场点上的声压是来自振膜各点的同向辐射相互叠加的结果
但是振膜各点到场点的距离不一致
因而计算近距离,或曰近场相位的时候,还要考虑这个叠加问题
...绕过了贝赛尔函数,不过按照我的普及能力,似乎绕不过多元微积分了
arch理论基础深厚!强!
延伸一下,当频率足够高时,辐射抗将远小于辐射阻,此时可以认为无限接近振膜表面的声压和质点速度是同相的!
-- 发布时间:2009-11-28 16:58:59
--
电信号有方波很正常,但声波真的有方波吗?即使近似的梯形波也是不存在的。方波电信号是平顶,对应着振膜在脉冲顶部的时间根本是处于静止状态,停止了对空气的策动,哪里还会产生声压?不管什么拾音器,方波电信号经动圈扬声器变换成声波都是成了猝发的尖峰波。
-- 发布时间:2009-11-28 23:53:48
--
以下是引用arch在2009-10-26 12:49:45的发言:
这个关于扬声器和传声器物理原理的问题很好,涉及到两者的详细物理背景
即使是熟悉物理知识的网友也可能一时反应不过来,“基础理论室”最需要的就是这样的帖子
在原帖里,作者提到电声和声电转换中涉及的声物理量问题;我理解这个问题
的确,从换能原理的公式出发,如电容式的位移转换为电压,一定是没错的
问题在哪?在于换能方式不是“声电”而是“声——力——电”
力学系统被原作者忽略掉了;而它自身是有个力阻抗的,跟电路里的电容、电感一样,有积分或微分的效果
实际上使用的多数声传感器捕捉的都是声压信号,路端电压的波形对应于声波波形;灵敏度说的都是dB/V
所以不存在所谓的“不同原理的传声器信号不好叠加”的问题,实际是不存在的
你理解的那个“积分”或“微分”的转换是通过力学部分的设计,通过控制质量、弹性和阻尼元件的相对关系来实现的
具体可参看《声学基础》1.5,或管老师的《电声技术基础》
换句话说,你的下面两个假设是不成立的:
“振膜置于声场中做受迫振动的运动状态与空气质点的振动完全一致”
“振膜的瞬时振幅,也就是空气分子的瞬时振幅”
这个成立的前提是系统没有弹性,质量为0,刚性无限大
紧贴振膜表面的那一层气体微元的运动状态倒的确是和振膜一致的
但是,这个运动状态受到了振膜本身的调制,并不是待测状态本身
空气微元的运动状态传递到振膜的运动状态,不是无条件的
具体发生什么变化,还取决于振膜的力阻抗
一个小错误是,扬声器所依据的基本换能原理是F=Bli
B——磁感应强度
l——音圈导线总长度
i——电流
U=BLV在这里仍然其作用,不过得到的是感生电动势
另一个小错误,扬声器振膜的质量相对较大,这个不是技术手段做不到更低
扬声器工作在所谓“质量控制区”,质量不能太低的
另外,回楼下的,俺怀疑你是否真把这个“走路问题”弄明白了,你至少没讲明白吧
[此贴子已经被作者于2009-10-27 21:16:20编辑过]
ARCH 大侠分析很不错,赞一个!
只是F=BLI中的L定义成有效长度似乎更严谨点!
另外,扬声器工作在“质量控制区”和振膜质量不能太低的不存在逻辑关系,扬声器作为被动发声器件,其自身的振动模态应该被很快的抑制,也就是说其振膜的惯性越小越好,从这点上来考虑我们是希望振膜质量变小,只不过工艺及材料的限制而不可能做小而已 .
[此贴子已经被作者于2009-11-28 23:56:01编辑过]
-- 发布时间:2009-11-29 0:06:31
--
以下是引用老兔子在2009-10-27 13:11:02的发言:
声压正比运动速度正比振幅正比压力
声压正比运动速度正比振幅正比压力
这个关系是不对的!
假设你这里定义的声压为接收点声压,运动速度为振膜的运动速度,振幅为振膜的振幅,压力为空气对于振膜的反作用力的话(我这么猜先),那么他们之间的关系应该是,声压正比于振膜运动速度和振动频率的乘积,运动速度正比于振膜振幅和振动频率的乘积,至于振幅和空气反作用力的关系比较复杂,当然你可以通过辐射阻抗反推回反作用力和振动速度的关系(实际上利用法向速度连续的原理,这个速度就是振膜表面空气质点的振动速度)
-- 发布时间:2009-12-1 11:56:43
--
以下是引用老兔子在2009-11-09 16:28:27的发言:
我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。
而我提出的理论重点是“动圈话筒振膜冲程想象成无限”“电容话筒振膜想象成无冲程”这样就能理解动圈话筒通过记录音圈移动速度同样是可以记录脉冲。
而你提出的什么声学的基本概念和我要论述的道理有关系吗?真的有关系吗?是不是真的有关系了?
我举例只是为了说明动圈话筒是可以记录脉冲,为了形象点并让人容易理解,所以假设了空气是刚性的。
而我提出的理论重点是“动圈话筒振膜冲程想象成无限”“电容话筒振膜想象成无冲程”这样就能理解动圈话筒通过记录音圈移动速度同样是可以记录脉冲。
而你提出的什么声学的基本概念和我要论述的道理有关系吗?真的有关系吗?是不是真的有关系了?
“我举例只是为了说明动圈话筒是可以记录脉冲”
提问者知道动圈可以记录脉冲
他问的不是这个,而是当电容给出方波的时候,动圈记录到的究竟“是什么”
我在3楼已经回答过,动圈记录到的同样是方波。他六楼下方的那个图错了,错在没有理解声接收的基本原理
您犯的是同样的理论错误——同时您还没有好好听题
“你提出的什么声学的基本概念和我要论述的道理有关系吗?真的有关系吗?是不是真的有关系了?”
声学基本概念跟“您论述的道理”没有关系;一旦有了关系,现有的声学理论就不自洽了
但是,声学基本原理和“我们讨论的问题”是相关的,真的是相关的,一定是相关的,必然是相关的,肯定是相关的,的确是相关的
为什么?
因为物理原理决定了可近似的范围。超过了这个范围,往同样方向迈出的一小步都是错误的
如果您了解了这些原理,就不会做你那几个“假设”,弄出个其实是耳道的模型,来证明你似是而非的“道理”
有个道理值得反复宣扬:声波的辐射和接收不是互逆过程。
扬声器做声辐射在各个场点上得到声压,而传声器做声接收是“弱水三千取一瓢饮”,只看单独一个场点的声压
所以扬声器和传声器的设计可以有本质的不同
这个道理可以解决很多问题,包括本帖讨论的这个问题
我的导师,某留洋的声学博士,也在这里迷糊过
另一个道理也值得反复宣扬:
先读题目再回答、先翻翻书再下断语是对别人的尊重,也是对自己的尊重
-- 发布时间:2009-12-1 13:22:22
--
以下是引用reqius在2009-11-28 16:58:59的发言:
电信号有方波很正常,但声波真的有方波吗?即使近似的梯形波也是不存在的。方波电信号是平顶,对应着振膜在脉冲顶部的时间根本是处于静止状态,停止了对空气的策动,哪里还会产生声压?不管什么拾音器,方波电信号经动圈扬声器变换成声波都是成了猝发的尖峰波。
电信号有方波很正常,但声波真的有方波吗?即使近似的梯形波也是不存在的。方波电信号是平顶,对应着振膜在脉冲顶部的时间根本是处于静止状态,停止了对空气的策动,哪里还会产生声压?不管什么拾音器,方波电信号经动圈扬声器变换成声波都是成了猝发的尖峰波。
只要正弦波能发出来,梯形波就是可以发出来的
-- 发布时间:2009-12-1 13:30:19
--
以下是引用中山门在2009-11-28 23:53:48的发言:
ARCH 大侠分析很不错,赞一个!
只是F=BLI中的L定义成有效长度似乎更严谨点!
另外,扬声器工作在“质量控制区”和振膜质量不能太低的不存在逻辑关系,扬声器作为被动发声器件,其自身的振动模态应该被很快的抑制,也就是说其振膜的惯性越小越好,从这点上来考虑我们是希望振膜质量变小,只不过工艺及材料的限制而不可能做小而已 .
[此贴子已经被作者于2009-11-28 23:56:01编辑过]
谢谢提醒,你关于音圈线的说法是更严谨的
另,设计扬声器的时候,出于瞬态响应的考虑,质量当然不能大
但出于谐振频率的考虑,质量太小则工作区遭到压缩
——弹性一定的情况下,质量小到一定程度,过渡到阻尼工作区,这里是有隐含的逻辑关系的
因此振膜质量不能是无限小的,我不认为这仅是由于材料和工艺的限制
-- 发布时间:2009-12-1 16:17:00
--
以下是引用寒山在2009-11-16 02:11:00的发言:
arch理论基础深厚!强!
延伸一下,当频率足够高时,辐射抗将远小于辐射阻,此时可以认为无限接近振膜表面的声压和质点速度是同相的!
谢谢吹捧。马克吐温说,他听到人说他句好话,能高兴仨月,我也是这种人
那部分叫做“同振质量”吧,做电路图的时候,是要算到模拟里去的
这个推导很可以锻炼数学啊,希望楼下“学习”的同学推导一下啊
每次看到有人跟帖说“学习了”的时候,我就在想“学到什么了呢?”
-- 发布时间:2009-12-5 11:38:20
--
收益匪浅,不过看起来晕呼呼的