主题：[原创]麦克风的心脏型指向性曲线讨论

有一种麦克风, 它的指向性图形是心脏形曲线, 这种曲线用x-y函数描述会非常复杂, 但是用极坐标方程则非常简单,

比如ρ=6(1-cosθ), θ∈［0,2π］就是一条心脏形曲线,

 

图像画在直角坐标系里, 如下所示:

 

此主题相关图片如下：cd30.jpg

 

我们来验证一下, 当θ等于零时, ρ=6(1-cos0)=6(1-1)=6*0=0,  曲线在坐标原点

θ等于90度角,也就是1/2 π时, ρ=6(1-cos 1/2 π )=6, 曲线与y轴的交点是(0,6)

θ等于180度角,也就是π时, ρ=6(1-cos π )=6(1-(-1))=6*2=12, 所以曲线与x轴负半轴交点是(-12,0)

方程与图形吻合得非常好, 图形很直观.

现在要求, 1) 该曲线围成的面积A,   2) 该曲线自原点(0,0)出发,逆时针方向绕行一周的周长C

 

因为曲线不是常规曲线, 所以需要用到积分, 从原点向曲线任意一点画一条射线, 射线的长度就是ρ,

现在让射线逆时针转动一个很小的角度, 假设是dθ, 那么射线扫过的面积将是一个小扇形,

这个小扇形的面积dA=1/2*ρ*ρdθ, 这里用到了求扇形的面积公式, 对dA进行积分, 积分曲间从零到2π,

所以

A=∫ 1/2*ρ*ρdθ  ｛0,2π｝

  =1/2 *∫ (6(1-cosθ))^2 dθ ｛0,2π｝

  =1/2 *36*∫ (1-2cosθ+(cosθ)^2)dθ ｛0,2π｝

  =18* [(θ|｛0,2π｝-2sinθ|｛0,2π｝+∫ (1/2+1/2*cos2θ)dθ ｛0,2π｝]

这里, 积分的第一项及第二项很简单, 积出来后直接写出, 第三项含cosθ的平方, 略作变换,化为简单形式, 也很容易求出,

最后cos2θdθ的积分, 在零到2π曲间上等于零, 同理sinθdθ 在零到2π曲间上也等于零, 所以最后只剩一三项有效

 

A=18*(θ+1/2θ) ｛0,2π｝

  = 18*3/2*θ｛0,2π｝

  = 18*3/2 *2π

  = 54π

( π是圆周率, 等于3.14159....)

 

太好了, 心脏形曲线的面积求出来等于54Pi.

 

再求周长, 仿效上面同样的方法, 过原点画射线, 让射线沿曲线转一个很小的角度dθ, 射线在曲线上划出的微小弧长是dl, 这段小弧的长度等于ρdθ, 则将dl从零到2Pi曲间上积分,就是弧长了

 

所以 C=∫ ρdθ  ｛0,2π｝

   =∫ 6(1-cosθ) dθ ｛0,2π｝

   这个积分十分简单, 将常数因子6提出, 第一项积分直接就是θ, 第二项的积分等于sinθ ,所以最后积分等于

   C=6* (θ-sinθ) | ｛0,2π｝

     =6*(2π- (sin0-sin2π))

第二项sinθ在零和2Pi弧度时都等于零, 所以心脏线的周长C=12π

 

但是仔细推敲一下, 会发现上面两个问题中有一个求错了. 哪里错了? 大家思考一下, 明天再来讲.

楼上几位都说得不错, 周长积分出错了. x轴负半轴可以放一个直径为12的圆进去, 圆心在(-6,0), 刚好能被心脏型完全包围进去,

而圆的周长是12Pi,所以心脏线的周长肯定大于12Pi的.   实际上面用极坐标求面积与周长的方法都有问题, 求曲线围成的面积与周长有几种方法, 后面我会陆续介绍. 其中用极坐标微分法(即前面的方法)是一种比较低级的方法, 它有它的适用范围, 超出了这个方法就无能为力了. 当然极坐标法也有它的好处, 比如它一般的算法可以比较简单, 最适合对付类似圆形状的较规则曲面, 它的应用条件是: 曲线围成的区域必须是凸曲域, 如果曲线含有拐点或凹面了, 那就不行了,会产生较大误差, 下面我贴的图片右上角有解释.

所以在不是凸曲域的情况下, 不能使用极坐标来微分. 所谓凸曲域也可以这样来判断: 如果曲面围成的面积内任意两点做连线, 这个连线上的所有点呢, 全部都包含在曲面之内, 那么可以说这个曲面是凸曲域. 用这个方法来检查一下前面的心脏线, 在心脏线右边, 作一条垂线, 可以看到垂线出了心脏线了, 然后又从心脏线上半部分进去, 所以心脏线不是凸区域.

 

实际上, 前文中用极坐标微分法求出的心脏线面积结果是对了, 但方法是错了, 这是因为歪打正着, 它在求面积的过程中产生了正误差和负误差, 两者之和正好为零(因为心脏线以x轴为对称轴), 所以最后答案对了, 但这样计算还是非常危险的, 应该避免.

 

苏格拉底说过, 没有验证的人生是不值得过的,所以我们对用这种方法求出的结果, 一定要进行验证.

要验证就要使用最准确的方法验证, 求 曲线长度最严密的方法是曲线积分, 这是非常强力的一种工具,非常有用.

子卿用计算机模拟的结果47.99....是对的, 但是不准确, 可能是近似误差原因. 周长正确答案应该是48,这种方法叫数值法, 也很有用.因为贴子里写数学符号实在是麻烦, 还不如手写快, 我将求心脏线周长的全部过程贴在下图.

 

 

继续分析心脏线, 前面已发现用极坐标算心脏线会出问题, 原因是心脏线围成的区域不是凸域, 当然, 这个区域仍然属于简单域, 所以可以用第1类曲线积分求解. 但是观察这个心脏线, 它奇怪之处是在原点方向发生了改变,也就是说它不是那么和谐, 从原点(0,0)出发, 分别向上和向下走把图形分成了两瓣, 正是这个地方使凸域发生了质的变化.心脏线在坐标原点(0,0)这个位置让人感觉很糟糕, 但是麦克风就比较喜欢, 因为此处麦克风的频率响应为零. 

 

事实上, 以上曲线积分求曲线的一类曲线积分方法是数学方法, 含义不是那么直观, 但是它的物理意义呢, 就比较好理解.

 

假设有一个人,它忽左忽右在平地上走, 那么他经过的轨迹是一条弯弯曲曲不规则的曲线, 如果他最后能回到出发点, 那么他走过的路线可以围成一个不规则的曲域(当然不一定是凸曲域), 但是我们要求他不能经过已经走过的路线, 也就是他不能踩他已经走出的轨迹, 这样他走出的曲面是一个简单域, 否则的话, 就是复杂域, 比如他走出一个8字形, 因为中间有两条轨迹相交了, 这样这个8字形将不是一个简单域.

 

这样, 这个人走过的轨迹画出了一条首尾重合的曲线, 我们称之为简单连通的闭合曲线, 这条闭合曲线的长度, 取决于两个因素, 一个是他行走的速度, 速度越快, 单位时间内走过了路程越远, 另一个是他行走的方向. 如果他一直不转弯, 走直线, 可以想象他可以走得无限远, 曲线将会无限长, 如果他很快就转弯了,最后回到出发点, 他走过的距离就越近.   这样速度加方向, 实际上可以看作一个量, 就是速度矢量,  如果他在任意某时刻速度是V,  V=V(t), V是时间t的函数, 在很小的单位时间元dt内他走过的路程等与速度乘时间,V=Vdt,

将这个小量在时间段上积分,比如从时间0时刻到最后他返回出发点的时间T积分, 就得到到他走过的总路程的长度.

所以 曲线周长=∫Vdt ｛0,T｝.

 

实际上他在某时刻的瞬时速度V,就是第一类曲线积分里的γ'(t), 第一类曲线积分里x=x(t), y=y(t)中的参数t,实际上就是时间, x与y就是运动物理某时刻的坐标位置, 当然在物理上可以这样理解, 如果是纯数学中, 不一定t非得代表时间, t就是一个纯粹的参数而已.

 

所以数学是很抽象的, 数学同物理相比较, 可以简单地概括为四个字"数在理前", 先有数学, 才有物理.

 

 

 回到心脏线的原点, 试求原点(0,0)处心脏线的切线, 在原点处它的切线似乎是x轴, 实际上,该点处的切线不存在. 

因为我们发现曲线可以由运动物体的速度表示, 曲线某点的切线方向, 等于运动物体在该点处的瞬间速度方向,

这很好理解,他的瞬间速度决定了他在那一点的运动方向. 所以求曲线某点的切线, 转化成求该点运动物的速度就行了.

在前面的曲线积分求周长过程里, 已经看到

x'(t)=6(-sint+sin2t), y'(t)=6(cost-cos2t), 这就是运动物体在某时刻t的瞬间速度, 沿着x轴,y轴的两个速度分量,

这两个分量的平方和再开根号就是速度大小. 那么要求在原点处的切线, 实际上就是t=0时刻的速度,

此时,将t=0代入, x'(-0+0)=0, y'(0)=6(1-1)=0, 太好了, 原来在原点出, 心脏线的速度是零, 也就是他没有任何方向,

所以他的切线不存在.

 

另外也可以这样理解, 在原点出心脏线连续, 但是导数不存在, 连续而不可导, 构成的点, 数学上称之为尖点,在尖点处有一些
奇怪的特性, 这个在国内高数教材里似乎没提过.实际上在尖点处, 曲线的速度为零. 为了更深刻地理解尖点, 我们再来看下面
的两个例子 

 

此主题相关图片如下：o9bd.jpg

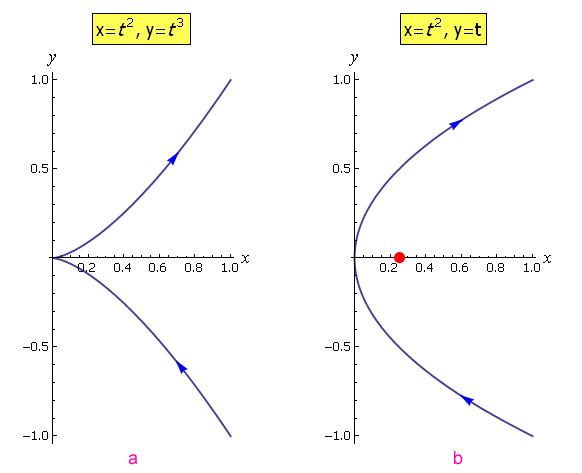
这是两个参数方程的图形, 图a是 x=t^2, y=t^3 的图像, 图b是x=t^2, y=t 的图像,也就是x=y^2,这是我们很熟悉的抛物线,

两个方程中的t的取值范围都是R.

 

这两个方程描述的问题看起来差不多, 实际上是一个物体从坐标第四象限的无限远出向原点(0,0)飞近, 到了原点刚接触到y轴就转向第一象限,继续向无限远飞行. 但他们的轨迹不太相同, 并且在原点处的感觉很不同. 第一个图形的转折很尖, 第二个图形的转折很圆滑.

 

实际上, 第一个图形里的(0,0)点就是尖点, 第二个图呢,不存在尖点. 因为图a中,

x'(t)=2t, y'(t)=3t^2, 在t=0处, 两个导数都是零, 所以速度是零, 切线也不存在,它在接近y轴的过程中,是先减速,然后远离y轴时加速.

 

而图b中,x'(t)=2t, y'(t)=1, 所以在原点处速度是(0,1),它的速度垂直向上, 指向y轴的正方向, 它的速度不为零, 可以是任意值.

所以它在原点出有切线, 切线就是y轴.

 

在真实的物理世界中, 图b描述的抛物线是天体运动的一种, 比如慧星造访太阳系, 它的轨迹就可以是一条抛物线,然后绕过太阳以后, 继续飞远离开, 它的速度在任意时刻都不可能是零.图b中的红点也标出了太阳的位置,在抛物线的焦点. 而在天体运动中, 图a的情况几乎不可能发生, 它好像是运动到某位置后,被某种障碍反弹出去,在反弹之前, 速度必须是零. 比如乒乓球往地面上斜抛,被地面弹出去, 就类似这种曲线. 这种现象一般在微观世界中才会出现, 比如微观粒子的运动等.

 

声学问题中经常出现图a的情况, 比如扬声器和麦可风的指向性图案中, 经常有很多的尖点, 特别是多瓣指向性图案中, 底部一下就是好几个尖点.这些尖点并不是那么受欢迎, 我们看上去感觉并不是那么良好, 因为含有尖点的图案我们认为它本身就是具有某些问题的, 不是那么和谐, 如果在频率响应里, 含有尖点的频响曲线, 会非常难听或刺耳, 但这些证明了声学中的问题反应了它属于微观世界里发生的现象.