Subwoofer design

1 - Box construction
My goal is to keep the box size as small as possible. The estimates show that a box with about 50 liter internal volume would lead to acceptable amplifier power requirements. Keeping the box small also makes it easier to construct a very stiff enclosure and to minimizes spurious sound output from panel vibration. 

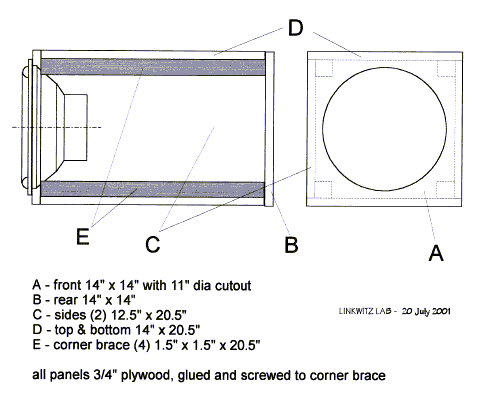
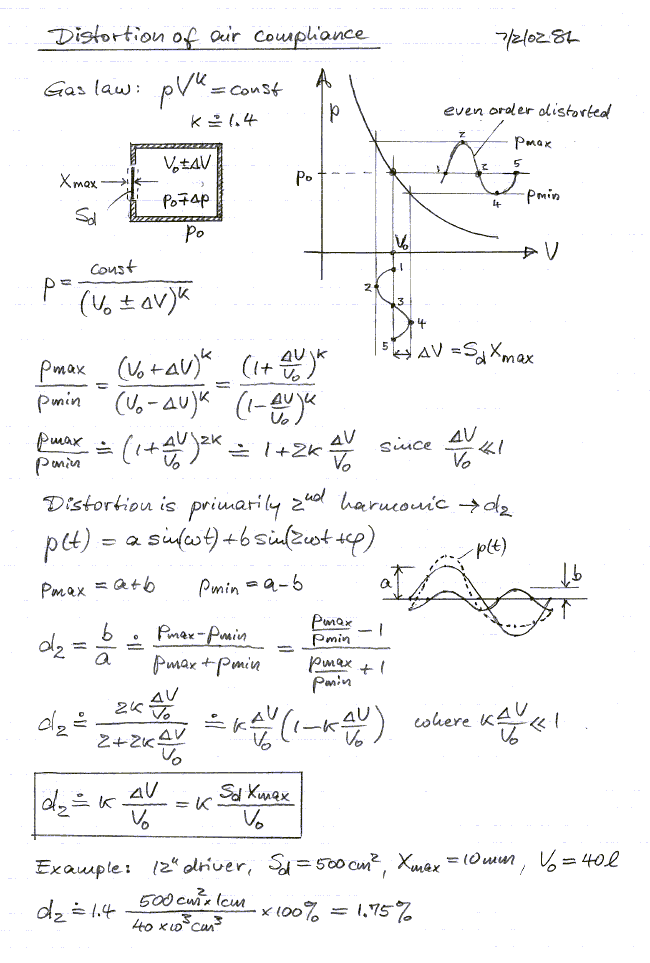
All joints are glued and strengthened with sheetrock screws. The driver is screwed to the front panel with a rubber gasket (neoprene weather stripping tape) under its flange. The box is completely sealed except for a small pin hole (<1 mm diameter) to equalize internal with external static pressure and to prevent displacing the cone from its normal resting position. No stuffing is used, to avoid nonlinear friction losses in case the material moves with cone displacement. The reduction in box resonance frequency that the stuffing could provide is not important, when the cut-off response is electronically controlled. The first internal air cavity resonance occurs when the 20.5" length equals 1/2 wavelength. This is at 330 Hz and far outside the frequency range of interest. The internal volume of the box is about 47 liter. The sound  can get extremely high, but the additional of the inside air upon the cone is small compared to distortion of the driver motor.
I use four self-stick rubber feet on the bottom of the box to prevent damage of the wooden floor and to avoid rattle.

 
此主题相关图片如下：


此主题相关图片如下：

2 - Driver and box model
It would be quite feasible to build a subwoofer simply by mounting a chosen driver in a box of acceptable size and measure its frequency response outdoors with a microphone at 0.5" in front of the dust cap. From this information one could then design an equalizer to obtain the desired response curve. 
It will be a more successful process, if you have some advance knowledge of what performance to expect from the driver and box combination and if you then measure the completed woofer to see if its response is as predicted. This requires a model. From the model you should also be able to predict the impedance that the amplifier sees, and the cone excursion for a given driving voltage, in order to calculate the power consumption as a function of frequency and SPL level. This allows decisions about driver selection and box size. 

The electrical model uses the force --> current (velocity --> voltage) analogy between mechanical and electrical impedances. The conversion from acoustical impedances (p/q) to mechanical impedances (F/v), which involves Sd, and the conversion from mechanical to electrical impedances (V/I), with the use of Bl, is described in books on electro-acoustics. The electrical impedance model looks like the following circuit with component values derived from the XLS 830500 driver specifications and a 47 liter box.  See closed-box1.xls for calculation of the values.

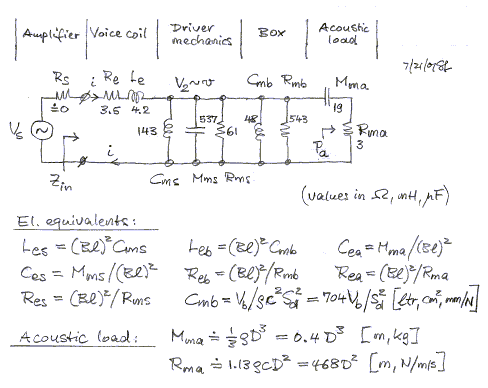
The circuit can be simplified by combining the two parallel inductors that represent driver and box compliance, and by combining the resistors for the viscous losses in driver and box. The reactance due to Le can be neglected at low frequencies compared to Re. Also, the power amplifier output resistance and speaker cable resistance Rs is insignificant when   compared to Re. The reactive component Mma of the complex acoustic radiation impedance is very small compared to the moving mass Mms of the driver. Also, the corresponding capacitive reactance is much larger than the radiation resistance Ra. Thus, both will be ignored. It is worth noting that the electrical power dissipated in Ra is the same as the acoustic power radiated for a given amplifier voltage Vs. From the radiated power it is easy to determine the sound pressure at some distance in free-space, via sound intensity and free-space impedance. The sound pressure can also be derived from the cone velocity v, which is proportional to the voltage V2. The circuit behavior is most conveniently analyzed with a program like CircuitMaker .
The above model is thus simplified to the following:

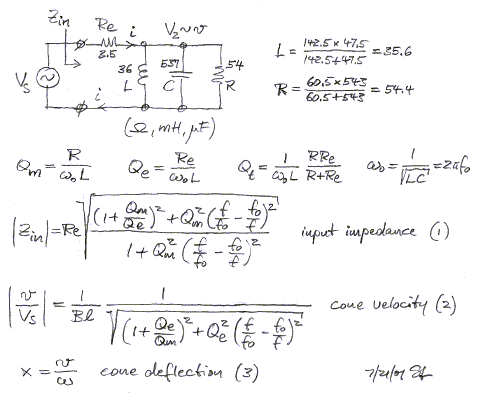
The derivation of formulas (1) and (2) from the circuit diagram takes a little effort using complex number algebra. At resonance, f = f₀, the circuit simplifies to two resistors, Re and R, which allows to determine the relationship between voltage V2 and velocity v. All these quantities are calculated in a spreadsheet. The derivations above are mainly given for a better understanding of the inner workings of the spreadsheet and of the use and limits for the model.

3 - Spreadsheet results
The purpose of the closed-box1.xls spreadsheet is to study the power requirements of a particular driver in a box of specified size. It is assumed that the driver has adequate cone excursion capability to provide the desired sound pressure level at the lowest frequency of its intended operating range. The maximally obtainable SPL can be determined from the spreadsheet spl_max1.xls , but is also calculated by 'closed-box1'. The different parts of the spreadsheet will be referred to by their page tabs [...], which are at the bottom of the closed-box1.xls display. Click on them.

Install the Excel 97/2000 Viewer on your computer, if you do not have access to the Microsoft Excel spreadsheet program. 

[Spec's] - Block 1 has the specifications of the XLS 830500. You can enter different driver parameters, but only change the bold faced numbers. Changing any other numbers will erase the underlying formulas. Note that if you enter VAS it will calculate Cms, in case this specification is not available.
Block 2 has the box data. The box Qb is set to a high value since there is no stuffing.
Block 3 gives the calculated driver parameters when mounted in the box.
Block 4 gives the values for electrical components of the simplified driver and box model.
The target response specification in block 5 will be need later to determine the necessary equalization together with the pole and zero locations that have been calculated for the model in 3a, 3b and the equalizer in block 6.

The results of the calculations are best observed in graphical format.

[Vp & Ip] - The curves show the required peak current and peak voltage from the power amplifier to obtain Xmax at different frequencies. The current has a minimum at the driver resonance. At low frequencies the amplifier is likely to run into current clipping before Xmax is reached. Reduce Vb to 23 liter, such as when a second driver is added at the other end of the box above, and you see how the current of each driver increases to unrealistic values. At frequencies above resonance the amplifier is likely to clip at its supply voltage. If the driver had a less strong motor with Bl = 10 N/A, then again the current demand on the amplifier would limit the maximum obtainable cone excursion.

[Power & SPL] - The SPL at 1 m increases at 12 dB/oct rate for constant excursion Xmax. Free-space is assumed. See Estimates for SPL in a room. Three power curves are shown. The middle one is the product of rms current and rms voltage in VA. The other two power curves show the 8 ohm power rating that an amplifier would have to have, in order to deliver the required peak current or peak voltage, that are necessary to reach Xmax. It is clear that Xmax is difficult to reach above the resonance frequency with typical amplifiers. Since the SPl is already high at these frequencies there is no need for such large excursions.

[SPL @ 2.83 V] - The graph shows the SPL frequency response of the driver mounted in the box for a constant drive voltage of 2.83 V, which would correspond to 1 W into 8 ohm. The actual amplifier load impedance differs completely from 8 ohm, but that is no problem for any well designed solid-state amplifier. The only limits are the amplifier's output current capability and maximum output voltage swing. The response shows a broad roll-off, as would be expected from the low Qt = 0.4. The woofer obviously needs equalization to be useful. If you enter Bl = 10 N/A for the driver, then the response shows the more typical highpass behavior, but the voltage sensitivity is reduced since the motor has less strength.

[SPL & Ip @ 10Vp] - Knowing a power amplifier's maximum output current and voltage swing this graph allows to estimate the maximum SPL that can be obtained when using it. The SPL can, of course, not exceed the excursion limited SPL from the [Vp & Ip] tab.
For example, a LM3886 power IC with Vp = 30V and Ip = 11.5A would give a voltage limited SPL that is 20 log(30V/10V) = 9.5 dB higher than shown and require 3 times the current indicated in the graph. This would be within the specifications of the LM3886, but whether 95.5 dB free-space SPL at 1 m and 40 Hz is sufficient, depends upon the application. Bridging two devices will double the voltage swing capability, but now has insufficient peak output current, unless two ICs are connected in parallel. Such parallel/bridged arrangement of ICs has to be carefully designed, to distribute the current drawn uniformly between the four devices. 

[Max SPL @ Vpeak] - The power amplifier to be used can be specified in Block 7 and the available peak voltage is calculated. For this peak voltage the maximally obtainable SPL is plotted. Typically, at low frequencies the SPL is excursion limited and Vpeak exceeds what is necessary. At higher frequencies the SPL becomes voltage limited, provided that the amplifier is capable of delivering the necessary peak current. 
If the same driver is used in an open baffle with path length D to form a dipole radiator, then the maximally obtainable SPL is determined from Fequal in Block 8. Be sure to set the internal box volume in Block 2 to a value much larger than the driver's VAS.

[Impedance] - The impedance of the driver by itself and in the box. When the calculated box impedance is compared to an actual measurement, one can get an idea of the box losses and of Qb.

The remaining two tabs, [Test] and [EQ], are discussed on the following pages.

Alternate drivers for the PHOENIX dipole woofer - 3

As I indicated in FAQ4 I have been trying to find a large excursion 12" driver that would give me twice the useable volume displacement as the 1252DVC or X6100 for 6 dB more acoustic output at about the same level of non-linear distortion. The cabinet size should increase only marginally and the cost of the driver should not more than double. This would allow me to obtain the same output with two such drivers in the PHOENIX woofer cabinet as I now get from four X6100 in a cabinet of twice its height.

Indeed, I found a driver that meets my requirements. It is the Peerless XLS series model 830500, a 12" (Sd = 466 cm²) unit with Xmax = 12.5 mm peak excursion. While other units on the market claim similar excursion capability, they usually suffer from excessive air turbulence and other noise at large displacements, which effectively reduces their useable excursion to 6 mm for open baffle applications.

The performance of the 830500 comes at the cost of lower sensitivity and early roll-off, as shown in comparison to the frequency response of the 1252DVC. All the following data are taken at about 2" from the dustcap of the unbaffled driver.

An analysis of the driver terminal impedance curve explains the roll-off behavior. The low Qts < 0.5 leads to real axis poles at 86 Hz and 4 Hz in the second order highpass polynomial and thus to the shallow 6 dB/oct roll-off.

Some example harmonic distortion measurements show the superior performance of the 830500. Second order distortion will be further reduced due to the driver arrangement in the PHOENIX woofer cabinet.

What the graphs do not convey properly is the audible improvement of the test tone cleanliness. This is especially remarkable for a 20 Hz tone at 1" p-p excursion. 

The amplifier requirements for excursions up to 1" p-p below 40 Hz are not too severe, because of the high, and somewhat capacitive driver impedance, (2) above.  At 20 Hz a 25.4 Vrms signal  across the 60 ohm driver impedance will produce 1" p-p excursion. That corresponds to 11 VA in power.
At higher frequencies, though, it takes considerable power to achieve 0.5" p-p and at 100 Hz even a 200 W/8 ohm amplifier will have difficulty to give more than 0.25" p-p.  
You can derive this from the graph below which gives the rms voltage necessary for 0.5" p-p excursion and the power in VA that the amplifier must deliver to the load (2).

The 1252DVC, in comparison, requires less power, but it is also limited in excursion before the driver misbehaves. For example, 0.5" p-p excursion is only obtainable below 40 Hz, because around 50 Hz the voice coil walks forward out of the gap at large signal levels. The useable displacement thus tends to 0.25" p-p for higher frequencies. Even so, around 80 Hz the cone has two conditionally stable rest positions and it is difficult to preserve a 0.25" p-p excursion. No such behavior was observed with the 830500.

In practice the amplifier power requirements are not quite as severe as it may seem from the graphs above. For an open baffle woofer the excursion falls off at (1/f)³ with increasing frequency for constant SPL. The real problems are distortion and insufficient output at the low frequency end.

Based on the measured data for cone excursion versus drive voltage and frequency, I made an estimate of the sound output at 1 m into half-space, if two of the 830500 are wired in parallel. The two drivers in parallel generate 6 dB more SPL than a single unit, but the amplifier has to drive an impedance that drops as low as 2.5 ohm at 100 Hz. I assumed an amplifier with 100 W into 8 ohm specification and sufficient current capability to deliver up to 200 VA into the varying speaker impedance. The analysis shows that such amplifier can drive the two 830500 to 1" p-p excursion only below 40 Hz before running out of power. Above 40 Hz the cone displacement is limited by the 200 VA of the amplifier.

With the two drivers in an open baffle of front-to-back spacing D=19" (483 mm) the resulting SPL increases from 68 dB and 25 mm p-p excursion at 10 Hz to 111 dB and 3.6 mm p-p at 100 Hz. A second woofer adds another 6 dB. These are quite respectable numbers.

Connecting the two drivers in series gives lower maximum SPL, because the cone excursion is limited at all frequencies by the 28.3 Vrms output voltage of the 100 W amplifier. SPL increases from 67 dB and 23 mm p-p excursion at 10 Hz to 107 dB and 2.3 mm p-p at 100 Hz. The minimum amplifier load impedance is now 10 ohm and might be more advantageous, if the amplifier has less output current capability.

Neither series nor parallel connection of the two drivers changes the low Qts. The corresponding early roll-off has to be equalized in addition to the normal 6 dB/oct open-baffle roll-off. The low Qts is an indication of the high motor strength and keeps drive requirements reasonable.

There are other alternatives available besides the 830500, which provide lower distortion than the 1252DVC/X6100, except that their useable maximum SPL is not significantly improved. See Woofer2.

Use of 830500 drivers for the PHOENIX woofer

The PHOENIX printed circuit board lacks the necessary circuitry to equalize the ~86 Hz roll-off due to the low Qts of the driver. A single MT1 circuit board can provide this equalization for two woofers. Details are included with the WM1/MT1 documentation. In addition, the MT1 pcb could also be used for a 100 Hz, 24 dB/oct woofer to midrange crossover, should that become desirable. 

Alternatively, the WM1 circuit board provides this capability and also allows correction of the 6 dB/oct dipole roll-off. Thus, using the WM1, two fully equalized dipole woofers can be built. They are easily crossed over and mated with any midrange units by using an additional  MT1 printed circuit board. 
Component values for equalizing a PHOENIX style woofer (see below) are included with the WM1/MT1 documentation. Also provided is specific information for equalizing an H-frame woofer cabinet for crossover frequencies up to 150 Hz. This is of interest when the H-frame acts as the base for another speaker that cannot be crossed over lower than 150 Hz. 

Dipole woofer cabinets for the 830500

The width of the cabinet could be reduced from 19.5" to 18" by changing the width of spacer F from 6" to 4.5". This will require installing the top driver while one side panel is removed and makes assembly more difficult. 
Great care must be taken during assembly that no particles fall into the exposed magnet gap behind the spider. The drivers are arranged for even order distortion reduction.

For a loudspeaker of the Beethoven-Grand or -Elite output level capability I recommend to use four drivers per side. If used with the PHOENIX, then the 100 Hz crossover should be 4th order for compatibility with the 21W/8554 and the increased excursions that might be demanded from it during very high playback volume levels. When four drivers are used, the two drivers in each of the stacked cabinets can be mounted for a cleaner front-to-rear acoustic path. In that case even order distortion reduction is obtained by reversing one of the cabinets as shown below.

楼上的楼上还有没有?顶!

还有,不过等你消化完了我再上传,呵呵!

为了大多数的人都能够看的，还是请楼主翻译先啦！

高!

叫楼主翻译太为难了!谢谢楼主!

文章在翻译中,过两天可传上来

 不错不错。

基本上是在LEAP和MLASS原版英文资料里面的相关公式上加以分解和引申阐述开来的。

能推敲到这个地步真的是花了很多的心思啊。